Pengertian Bilangan Prima, Fakta, Metode, Sejarah, Contoh

Apa Itu Bilangan Prima?

Bilangan prima adalah bilangan yang lebih besar dari 1. Mereka hanya memiliki dua faktor, 1 dan bilangan itu sendiri. Ini berarti angka-angka ini tidak dapat dibagi dengan angka apa pun selain 1 dan angka itu sendiri tanpa meninggalkan sisa.

Bilangan yang memiliki lebih dari 2 faktor disebut bilangan komposit.

Pengertian Bilangan Prima,  Fakta, Metode, Sejarah, Contoh 

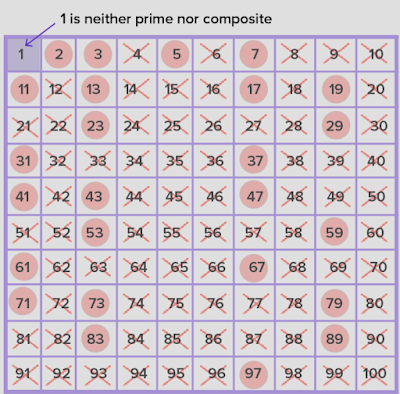
Saringan Eratosthenes (Metode Mencari Bilangan Prima)

Pada abad ketiga SM, ahli matematika Yunani Eratosthenes menemukan metode yang sangat sederhana untuk menemukan bilangan prima.

Ikuti langkah-langkah yang diberikan untuk mengidentifikasi bilangan prima antara 1 dan 100.

Langkah 1: Buat seratus bagan.

Langkah 2: Tinggalkan 1 karena ini bukan bilangan prima atau bilangan komposit.

Langkah 3: Lingkari 2 dan coret semua kelipatannya karena bukan bilangan prima.

Langkah 4: Lingkari angka yang tidak disilang berikutnya, yaitu 3, dan coret semua kelipatannya. Abaikan angka yang sebelumnya dicoret seperti 6, 12, 18, dan seterusnya.

Langkah 5: Lanjutkan proses melingkari bilangan yang tidak disilang berikutnya dan mencoret kelipatannya sampai semua bilangan pada tabel dilingkari atau dicoret, kecuali 1.

Saringan Eratosthenes (Metode Mencari Bilangan Prima)

Fakta Bilangan Prima

1. Satu-satunya bilangan prima genap adalah 2. Semua bilangan genap lainnya dapat dibagi dengan 2.
2. Jika jumlah digit angka adalah kelipatan 3, angka tersebut dapat dibagi dengan 3.
3. Tidak ada bilangan prima yang lebih besar dari 5 yang diakhiri dengan angka 5. Angka apa pun yang lebih besar dari 5 yang diakhiri dengan angka 5 dapat dibagi dengan 5.
4. Nol dan 1 tidak dianggap sebagai bilangan prima.
5. Kecuali untuk 0 dan 1, suatu bilangan adalah bilangan prima atau bilangan komposit. Bilangan komposit didefinisikan sebagai bilangan apapun, lebih besar dari 1, yang bukan bilangan prima.

Sejarah Singkat Bilangan Prima

Ternyata, bilangan prima memiliki sejarah yang panjang dan sudah dikenal sejak lama sekali. Dari catatan yang ditemukan, diketahui bilangan prima telah dipelajari pada tahun sekitar 300 sebelum masehi oleh matematikawan Yunani bernama Euclid of Alexandria.  Beliau menyatakan bahwa bilangan prima tidak terbatas. Sekitar seratus tahun setelahnya, ilmuwan Yunani lainnya bernama Eratosthenes of Cyrene menemukan metode screening dalam mengidentifikasi bilangan prima pada daftar tertentu.

Setelah studi yang dilakukan ilmuwan Yunani tadi, studi mengenai bilangan prima tidaklah terlalu banyak berkembang. Perkembangan pesat terjadi pada abad ke 17 ketika seorang biarawan Prancis bernama Marin Mersenne yang mendefinisikan bilangan prima dalam rumus di bawah ini.

Contoh Bilangan Prima

Dalam menentukan apakah suatu bilangan merupakan bilangan prima atau bukan adalah menggunakan faktor bilangan. Faktor adalah bilangan yang bisa habis membagi suatu bilangan, seperti faktor dari bilangan 6 yang habis dibagi oleh bilangan 1, 2, 3 dan 6. Kesimpulannya faktor dari bilangan 6 adalah 1, 2, 3 dan 6, tapi bilangan 6 bukan termasuk dalam bilangan prima.

Karena memiliki faktor lebih dari 2 yakni 1, 2, 3 dan 6, bilangan prima ditentukan dengan faktor yang tidak lebih dari 2 yakni bilangan satu dan bilangan itu sendiri. Contoh bilangan prima adalah bilangan 7, faktor bilangan ini adalah 1 dan 7. Artinya bilangan tujuh akan habis jika dibagi dengan bilangan 1 dan bilangan itu sendiri.

Hampir semua bilangan prima adalah bilangan ganjil, meskipun ada satu bilangan genap yang masuk ke dalam daftar. Bilangan 2 menjadi satu-satunya bilangan genap dalam daftar bilangan prima, karena faktor dari bilangan 2 yakni 1 dan bilangan 2 itu sendiri. Contoh lain bilangan prima kurang 10 di antaranya 3, 5 dan 7.

Sekian artikel Matematika mengenai Pengertian Bilangan Prima,  Fakta, Metode, Sejarah, Contoh  dari Konsep Edukasi semoga artike matematika ini dapat membantu dan bermanfaat untuk kamu yang sedang mempelajari bilangan prima.